Az egyszerre matematikai és geográfiai probléma megoldása nem is olyan egyszerű: hosszas próbálgatás után jött rá két indiai kutató, Rohan Chabukswar és Kushal Mukherjee. A számítás még komputerrel is nehézkes, mert a kalkulációt megzavarja a partvonalak szeszélyessége, és a lehetséges útvonalakon minduntalan felbukkan egy sziget vagy más szárazföld, netán jégpáncél, ami miatt el kellene térni az egyenes vonaltól.
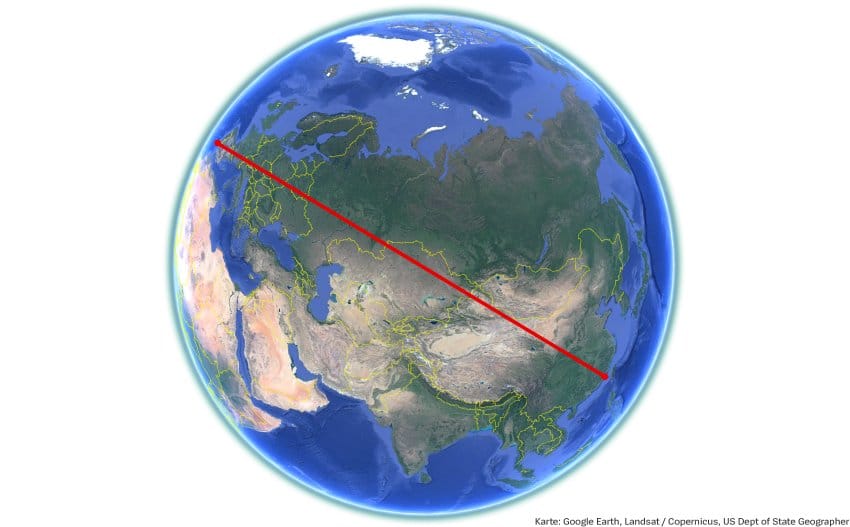
A száraz lábbal megtehető út tervezését az útba eső tavak és folyók bonyolítják. Azt hamar felismerték, hogy a vonalnak egy főkörön (az Egyenlítőhöz hasonló átmérőjű körön) kell húzódnia. Az azonban még számítógéppel is megoldhatatlannak bizonyult, hogy az összes főkört megvizsgálják. (Az amerikai óceánkutató intézet, a NOAA Föld-modelljének felbontása olyan alapos, hogy több mint 233 millió főkör létezik rajta.) Inkább a branch-and-bound módszert választották: az ígéretesnek tűnő útvonalakat részekre bontották és úgy elemezték. Így igazoltak egy pár évvel korábbi feltételezést: a mintegy 32 ezer kilométeres tengeri utat Pakisztán és Kamcsatka között.
A megszokott világtérképen ez kanyargósnak látszik, de a földgömbön nyílegyenes – eltekintve persze a Föld görbületéből adódó függőleges eltéréstől. Hasonló módon kimutatták, hogy a leghosszabb szárazföldi út 11 241 kilométer, és Kína keleti partjától Portugáliáig szeli át Eurázsiát. Akadt korábbi számítás, amely hosszabb utat kalkulált, de az nem tehető meg száraz lábbal, mert át kellene kelni hozzá a Holt-tengeren.
A cikk a HVG 2018/20. számában jelent meg.