Mintegy 2000 éven át senkinek sem sikerült megcáfolnia egy háromszögekre vonatkozó állítást, két japán egyetemista azonban előállt az áttörést jelentő számítással.
A matematika nemcsak azért szép, mert bizonyos esetekben gyönyörű a dallama, hanem azért is, mert még több ezer éves története ellenére is vannak olyan tételei/problémái, amelyek megoldásra várnak. Már eggyel kevesebb ilyen létezik, a japán Keió Egyetem két diákja ugyanis megoldott egy nagyjából 2000 éves problémát.
Azt már az ókori görögök óta gondolják a matematikusok, hogy létezik olyan, derékszögű és egyenlő szárú háromszögből álló páros, melyek tagjainak kerülete és területe is megegyezik. Ám ezt az elméletet azóta sem sikerült senkinek bizonyítania. Egészen idén őszig: a tokiói Keió Egyetem harmadéves hallgatója, Macumura Hideki és másodéves doktorandusza, Hirakava Josinoszuke a Journal of Number Theory című tudományos szaklapban közölte azt a tanulmányt, amely pontot tesz az ügy végére – jelentette a SoraNews24.
A probléma alapja a háromszög területszámítási módszere. A háromszög területét az ismert képlet alapján – (a x ma)/2 – számítjuk ki, ahol az a a háromszög egyik oldalának, az ma pedig az ehhez tartozó magasságvonal hossza. Ha egy derékszögű és egy egyenlő szárú háromszög kerülete megegyezik, a területszámításnál használt magasságvonal hossza miatt a területük eltér egymástól. A két japán matematikus viszont azt az ókori görög sejtést akarta bebizonyítani, hogy létezik egy olyan háromszög-páros, amelynél a kerület és a teürlet is megegyezik.
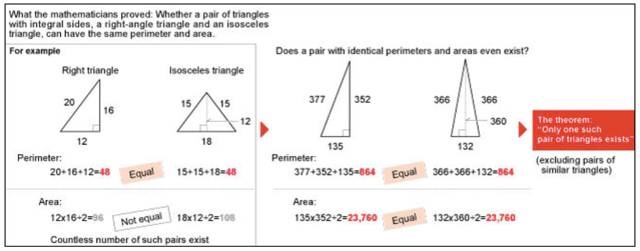
A japán matematikusok ennek bizonyításához az úgynevezett Diofantoszi geometriát használták. Az itt található nem hosszú, de bonyolult levezetéssel sikerült megcáfolniuk azt az állítást, miszerint nem létezhet a fent említett háromszögpáros. Vagyis: sikerült megtalálniuk az egy olyan derékszögű és egyenlő szárú háromszög-párost, amelynek a kerülete és a területe is megegyezik. Ezek alapján a derékszögű háromszög rövidebb befogója 135, a hosszabbik befogója 352 egység kell, hogy legyen, míg az átfogója 377 egység. Az egyenlőszárú háromszög esetében pedig 132 egység hosszú az alap, míg a háromszög két szára egyaránt 366-366 egységnyiek. Az a oldalhoz tartozó magasság 360 egység. Ezekből az adatokból pedig könnyen kiszámolható, hogy a háromszögek kerülete 864, míg a területük 23 760 egység.
Hogy ez a bizonyítás mire lesz jó a jövőben, azt egyelőre nem lehet tudni. A matematikában viszont pont ez a szép: a felfedezések sosem önmagukban érdekesek, az mindig a jövőben derül ki, mire is lehet használni őket.
Ha máskor is tudni szeretne hasonló dolgokról, kövesse a HVG Tech rovatának Facebook-oldalát.
Évtizedes, közmegegyezésen alapuló kollektív politikai hazugságot törvényesített az Országgyűlés kormánypárti többsége azzal, hogy gyorsított eljárásban elfogadta néhány KDNP-s politikus semmiből felbukkant ötletét a kampányköltések felső korlátjának eltörlésére. A módosítás mögött többféle politikai szándék is felsejlik.
Budapest megkapta az azonnali jogvédelmet is.
Ellenzéki össztűz zúdult a Parlamentben a miniszterelnökre.
Ahogy ígérték, az Európai Bizottság bemutatta az orosz gáz és olaj importjának megszüntetésére vonatkozó javaslatát.
A hatóságok vizsgálják, hol kaphatta el a súlyos betegséget.
Egyikük negyven év börtönt kaphat.
Az államtitkár Csendes Olivért jelentős nemzetközi tapasztalattal rendelkező vezetőként jellemezte.
