Három évtizednyi keresgélés és némi szuperszámítógépes kapacitás segítségével a matematikusok végre újabb Dedekind-számot találtak. Hogy rögtön a lényeggel kezdjük, erről van szó:

286 386 577 668 298 411 128 469 151 667 598 498 812 366.

Szép, ugye? És jó hosszú is. 42 számjegyből áll, és csupán a kilencedik Dedekind-szám a D(9), amit sikerült felfedezni. Az előző legnagyobbat, a D(8)-at még 1991-ben találták meg, az 23 számjegyből állt. Az eddig megtalált számok az alábbiak:

• D(0) = 2
• D(1) = 3
• D(2) = 6
• D(3) = 20
• D(4) = 168
• D(5) = 7581
• D(6) = 7 828 354
• D(7) = 2 414 682 040 998
• D(8) = 56 130 437 228 687 557 907 788.

A Dedekind-számot nem csak kiszámolni nehéz, hanem már megérteni sem egyszerű. Lennart Van Hirtum, a németországi Paderborni Egyetem kutatója szerint olyan hatalmas számokkal kell dolgozni, hogy sokáig az is kérdéses volt, a kilencediket sikerül-e egyáltalán valaha megtalálni.

A Dedekind-számok kiszámításához a logikai függvények törvényszerűségeit kell ismerni. Képzeljünk el egy gépet, amibe csak két bemeneti adatot tudunk megadni, a gép pedig ezekből választ egy kimenetet – például bedobjuk a gépbe, hogy egy állítás igaz vagy hamis, az pedig eredményül egyiket vagy másikat fogja adni. De beszélhetünk a számítógépek alapvető működését meghatározó 0-ról és 1-esről is, mint bemeneti információ, a lényeg ugyanaz.

Ehhez képest a monoton logikai függvények olyan logikai függvények, amelyeknél ha változtatunk a bemenő adatokon, akkor a kimenő eredmény is ugyanúgy fog változni. Vagyis ha a bemenetnél a 0-át 1-re cseréljük, akkor a kimenetnél is 0-ról 1-re fog változni az eredmény, 1-ről 0-ra sosem – magyarázza a SicenceAlert. A monoton logikai függvények műveletei közé tartoznak az ÉS (∧) és a VAGY (∨) műveletek.

A Dedekind-számoknál a kutatók ezt piros és fehér színnel jelölték, nem pedig 0-val és 1-esekkel, de a lényeg ugyanaz. Az alábbi ábrán a D(0), a D(1), a D(2) és a D(3) láthatók.

University of Paderborn

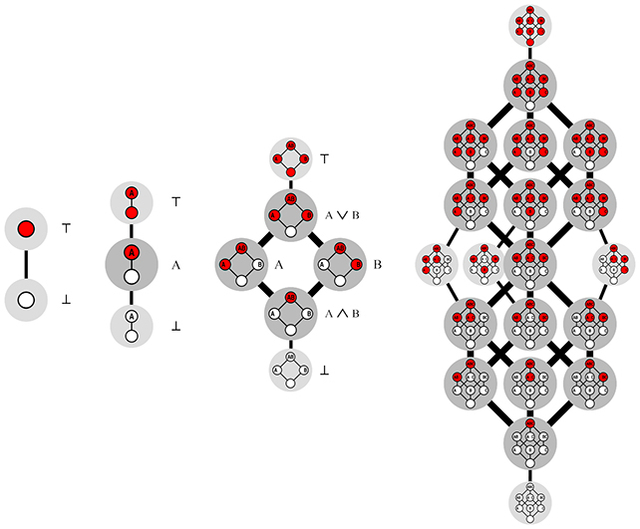
A fenti ábrát úgy is elképzelhetjük, hogy van egy n-dimenziós kockánk. (Az n a dimenziók számát jelöli. Ha n=3, akkor háromdimenziós kockáról beszélünk, ami gyakorlatilag a hagyományos dobókockának felel meg). Ezt a dobókockát állítsuk az egyik sarkára, majd a többi sarkát színezzük pirosra vagy fehérre. Alapvetően egy szabály van: sosem szabad egy fehér sarkot a piros pont fölé helyezni. A lényeg, hogy a végén megszámoljuk, ez hány különböző módon lehetséges.

1991-ben a Cray-2 szuperszámítógépnek – az akkori egyik legerősebb szuperszámítógépnek – és Doug Wiedemann matematikusnak 200 órájába telt, hogy kiszámítsák a D(8)-at. A most felfedezett D(9) majdnem kétszer olyan hosszú szám lett, mint a D(8) volt.

A kiszámításához egy speciális szuperszámítógépre volt szükség: olyanra, ami a felhasználás helyén programozható logikai kapumátrixokat használ (Field Programmable Gate Array, FPGA). Ez párhuzamosan több számításon is tud dolgozni. Így esett a választás a Noctua 2 nevű szuperszámítógépre. Bár a számítógépen fejleszteni is kellett, így is öt hónapba telt, mire sikerült megtalálni a D(9)-et. Hogy a D(10)-re mikor derülhet fény, nem tudni, de könnyen lehet, hogy még 32 évet kell rá várni.

A Dedekind-számok egyébként az 1916-ban elhunyt német matematikusról, Richard Dedekindről kapták a nevüket.

Ha máskor is tudni szeretne hasonló dolgokról, lájkolja a HVG Tech rovatának Facebook-oldalát.